Definitions and Physical Models
- Complement
- GC Content
- Length
- Melting Temperature (ANALYZE function)
- Melting Temperature (TM MISMATCH function)
- Mixed Bases Definitions
- Modifications
- Molar Extinction Coefficient
- Molecular Weight (Anhydrous)
- nmole/OD260
- Problem
- Secondary Sequence
- Sequence
- µg/OD260
The complementary sequence to the entered oligonucleotide, which is shown in 5' to 3' orientation and in DNA format. Modifications are ignored when the complementary base is determined. However, for modifications that are native base analogs, the complementary base is the native base. Complementary base to inosine is cytosine.
GC ContentThe molar percentage of guanine and cytosine bases in an oligonucleotide sequence.
LengthNumber of bases in the analyzed oligonucleotide sequence.
Melting Temperature (ANALYZE function)Melting temperature (TM) is the temperature at which an oligonucleotide duplex is 50% in single-stranded form and 50% in double-stranded form. The Oligo Analyzer estimates TM from the nearest-neighbor two-state model, which is applicable to short DNA duplexes,
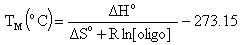
where 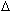 H° (enthalpy) and
H° (enthalpy) and  S° (entropy) are the melting parameters calculated from the sequence and the published nearest neighbor thermodynamic parameters, R is the ideal gas constant (1.987 cal
S° (entropy) are the melting parameters calculated from the sequence and the published nearest neighbor thermodynamic parameters, R is the ideal gas constant (1.987 cal K-1mole-1), [oligo] is the molar concentration of an oligonucleotide, and the constant of -273.15 converts temperature from Kelvin to degrees of Celsius. The most accurate, nearest-neighbor parameters were obtained from the following publications for DNA/DNA base pairs
(Allawi,H., SantaLucia,J.,Jr., Biochemistry, 36, 10581), RNA/DNA base pairs (Sugimoto,N. et al., Biochemistry, 34, 11211), RNA/RNA base pairs (Xia,T. et al., Biochemistry, 37, 14719), and LNA/DNA base pairs (isolated LNA bases follow McTigue,P.M. et al., Biochemistry, 43, 5388, consecutive LNA bases follow Owczarzy,R et al., Biochemistry, 50, 9352).
K-1mole-1), [oligo] is the molar concentration of an oligonucleotide, and the constant of -273.15 converts temperature from Kelvin to degrees of Celsius. The most accurate, nearest-neighbor parameters were obtained from the following publications for DNA/DNA base pairs
(Allawi,H., SantaLucia,J.,Jr., Biochemistry, 36, 10581), RNA/DNA base pairs (Sugimoto,N. et al., Biochemistry, 34, 11211), RNA/RNA base pairs (Xia,T. et al., Biochemistry, 37, 14719), and LNA/DNA base pairs (isolated LNA bases follow McTigue,P.M. et al., Biochemistry, 43, 5388, consecutive LNA bases follow Owczarzy,R et al., Biochemistry, 50, 9352).
TM calculations for oligonucleotides containing non-consecutive, isolated LNA nucleotides hybridized to a DNA template utilize LNA energetic parameters from McTigue,P.M. et al. Consecutive LNA bases on a DNA template use parameters from Owczarzy,R et al. LNA nucleotides on an RNA template are approximated because nearest-neighbor parameters for these specific combinations are not yet available.
TM depends on the monovalent and divalent salt concentrations ([Na+] and [Mg++], respectively) of the solvent.
Linear TM corrections were previously used to model the effects of cations on DNA hybridization. However, scientists at IDT determined that these linear functions are inaccurate. We have developed new functions from several thousand ultraviolet and calorimetric melting experiments for over 100 short DNA duplexes in a variety of sodium, potassium, and magnesium buffers.
OligoAnalyzer employs the improved TM salt correction function for monovalent (Na+) ions (Owczarzy,R. et al., Biochemistry, 43, 3537),
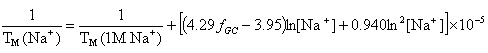
and for divalent (Mg++) ions (Owczarzy, R. et al., Biochemistry, 47, 5336),
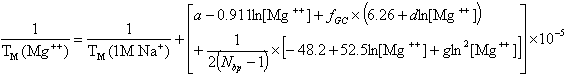
where fGC is the fraction of GC base pairs and Nbp is the number of base pairs. The monovalent ion or the divalent ion correction equations are used depending on the following ratio R of [Mg++] and [Na+].
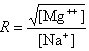
If R < 0.22, the monovalent ion correction is employed otherwise the divalent correction is used, including the case when [Na+] is zero. If R value is in the range from 0.22 to 6.0, the divalent ion correction is applied using a, d, and g coefficients that varies with Na+ concentration. These coefficients are constant for higher values of R (the second column of the following table).
| Variables adjusted to account for monovalent effects | Constants | |
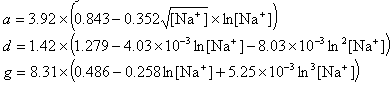 |
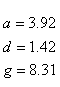 |
Deoxynucleoside triphosphates (dNTPs) affects the concentration of free divalent ions that enters into the above correction functions and the calaculations of the ratio R. Free magnesium concentration is predicted from total Mg++ concentration, [tMg++], using relationships developed from the equilibrium binding constant of Mg++ and dNTPs.
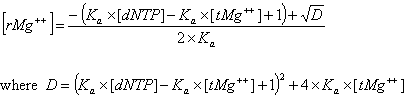
The association constant Ka is about 3x104 in biological buffers. These new parameters and methods are implemented within the OligoAnalyzer and improve the melting temperature accuracy, especially for standard PCR conditions. In the current version, however, these new parameters (Mg++ and dNTP concentrations) are defaulted to 0.0 mM, so that predicted melting temperature are identical to values predicted by the previous version of the OligoAnalyzer. To take advantage of these new, more accurate methods, the values for [Mg++ ] and [dNTP] concentrations must be specified.
Target Type list has two possibilities DNA or RNA. Default type is DNA.
Oligo Conc box is used to enter oligo concentration ([oligo]) and has a range from 10-4 µM (100 pM) to 105 µM (100 mM). Default [oligo] is 0.25 µM, which is typically used in biological applications. Oligo concentration is assumed to be significantly larger (at least 6x) than concentration of the complementary target, which is true in majority of molecular biology experiments. If this is not a case, concentrations of both strands of the duplex must be considered and you should enter in the Oligo Conc box,
[oligo] = [strand1] – [strand2]/2 when [strand1] 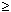 [strand2]
[strand2]
[oligo] = ([strand1] + [strand2])/4 when [strand1] = [strand2]
If the oligo sequence is selfcomplementary, enter total oligo concentration in the Oligo Conc box and TM will be accurately predicted. Because target and the oligo are the same chemical species, target concentration is unnecessary to consider for selfcomplementary oligomers.
Na+ Conc box is used to enter total monovalent ions concentrations (Na+, K+, Tris+) in the range from 5 mM to 1500 mM (1.5 M). Default concentration is 50.0 mM.
Mg++ Conc box is used to enter total divalent ions concentration [tMg++ ] in the range from 0.01 mM to 600 mM; however this concentration cannot be lower than the oligo concentration multiplied by the number of base pairs. Default Mg++ concentration is 0.0 mM.
dNTPs Conc box is used to enter total deoxynucleoside triphosphate concentrations (dNTPs) and in the range from 0.0 mM to 1000 mM (1.0 M); however the [dNTP] may not exceed 120% of the Mg++ concentration. Default dNTP concentration is 0.0 mM.
See mixed bases and modifications below for their effects on TM.
Click here for further information regarding melting temperature.
A TM MISMATCH function predicts thermodynamics of DNA molecules containing a single base mismatch and compares the result with the perfectly matched duplex. This is useful for estimating the mismatch discrimination and design of probes to detect single nucleotide polymorphisms (SNPs) where the allelic forms of a gene sequence might differ at only a single base position.
The most accurate nearest-neighbor parameters are applied to predict melting temperature of a DNA oligo that is hybridized to a DNA template with and without a single base mismatch (SantaLucia and Hicks, Annu. Rev. Biophys. Biomol. Struct, 33, 415–440). Overhangs (dangling ends) of the target strand are explicitly considered and this improves predictions for the annealing of oligo to a long DNA target sequence (Bommarito,S. et al., Nucleic Acids Res., 28, 1929-1934).
The melting temperatures of the exactly complementary target and the single base mismatch target are calculated using a two-state model,

where [strand1] and [strand2] are concentrations of single strands entered in the Oligo Conc box and the Target Conc box, and [strand1] ≥ [strand2]. The Target Conc box accepts values from 0 µM to 105 µM (100 mM). Default target concentration is 0 µM, which should be used for hybridization of oligo its genomic target of unknown low concentrations. The exact complement TM reported by the TM MISMATCH function could be slightly different from the TM calculated by the ANALYZE function because of additional dangling end interactions and nonzero target concentration, which are not accounted in the standard TM reported by the ANALYZE function.
Hybridization Temperature is the temperature, in degrees of Celsius, at which the percent of the single strand bound to the target is calculated.
Hybridization Percent Bound reports the percent of the exact complement and the single base mismatch sequences, which are expected to be annealed to target at the specified hybridization temperature. Percent bound ( ) is calculated from the following equation (Owczarzy,R. Biophys. Chem., 117, 207-215),
) is calculated from the following equation (Owczarzy,R. Biophys. Chem., 117, 207-215),

where Ka is the association equilibrium constant obtained from predicted thermodynamic parameters,
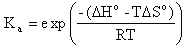
The T is the hybridization temperature in Kelvins. If the hybridization temperature is chosen to be the TM of the exact complement then its percent bound ( ) will always be 50% because that is set in the definition of melting temperature.
) will always be 50% because that is set in the definition of melting temperature.
Mixed bases, which are also known as degenerate or wobble bases, can be introduced at any position of oligomer sequence. For example, mixed base composition at a single position can include all 4 bases ("N"), C or T bases, ("Y"), A or G bases ("R"), etc. Since there are 11 different possible combinations of 2, 3 or 4 bases, a universal nomenclature has been established that must be used when specifying nucleic acid content at a mixed base site.
Oligo Analyzer and IDT ordering system use standard definitions (IUB codes):
| Symbol | Mixed bases |
| R | A, G |
| Y | C, T |
| M | A, C |
| K | G, T |
| S | C, G |
| W | A, T |
| H | A, C, T |
| B | C, G, T |
| V | A, C, G |
| D | A, G, T |
| N | A, C, G, T |
Oligomer orders synthesized using mixed base sites result in a product that is a heterogeneous mixture of distinct oligomeric species. Species have different bases at the mixed sites. Therefore, they have different
molecular weight, melting temperature (TM), and extinction coefficient (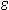 260) values. Rather than reporting the various values for each of the component species, a single value is given that estimates the population average from all species present. Molecular weight calculations are made using the average base content. Melting temperature is calculated by averaging nearest-neighbor enthalpy (
260) values. Rather than reporting the various values for each of the component species, a single value is given that estimates the population average from all species present. Molecular weight calculations are made using the average base content. Melting temperature is calculated by averaging nearest-neighbor enthalpy (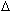 H°) and entropy (
H°) and entropy (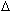 S°) values at each mixed site. Extinction coefficient is similarly predicted by averaging nearest-neighbor values at mixed sites.
S°) values at each mixed site. Extinction coefficient is similarly predicted by averaging nearest-neighbor values at mixed sites.
Further, the minimum and maximum TM of the oligomer mixture is also derived using the IDT proprietary TMExtreme algorithm. The method uses the nearest-neighbor thermodynamic model and the unified set of parameters (Allawi,H., SantaLucia,J.,Jr., Biochemistry, 36, 10581), however, it avoids the slow calculations of each possible oligomer. The TM range is calculated in 5 - 10 msec. Predictions of TM range are accurate with an average deviation of  0.5 °C in comparison with the complete TM calculations for all possible oligomers in the mixture.
0.5 °C in comparison with the complete TM calculations for all possible oligomers in the mixture.
Modified oligonucleotides also need special consideration to ensure accuracy when calculating molecular weight, extinction coefficient (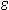 260), and melting temperature (TM). Modifications can change oligo mass, and sometimes alter UV absorbance or TM.
260), and melting temperature (TM). Modifications can change oligo mass, and sometimes alter UV absorbance or TM.
Examples:
Molecular Weight of an oligo containing an NHS Ester modification (such as 5' Texas Red NHS ester) is a sum of molecular weights of native oligo, the fluorophore group, and an amino modifier.
Extinction Coefficients (
260) of modifications, such as fluorophores and base analogs, are usually added to the
260 of the native oligonucleotide. Calculations for base analogs (e.g., 5-bromo dC) and conjugated bases (e.g., fluorescein dT) are more complex. First,
260of an oligo containing the unmodified base are calculated. Adjustment is later added for the contribution of the modification (fluorophore). Unfortunately,
260 values are not known for all modifications.
Melting Temperature (TM) can be changed when nucleotides are modified or additional chemical groups are added. For example, introduction of phosphorothioated residues decreases TM significantly. In contrast, LNA nucleotides increase TM. Unfortunately, nearest neighbor thermodynamic parameters have not been determined for majority of these modifications. Therefore, no accurate parameters and physical models exist that would allow us to calculate melting temperatures for many modified oligonucleotides. Internal base modifications, e.g. biotin-dT, could collide and interfere with the duplex structure. Because the quantitative effects of interference are unknown, they are neglected. If thermodynamic parameters are not available, Oligo Analyzer reports TM values for the unmodified sequence. Melting temperature changes caused by modifications may be approximated from the published literature. If needed, a precise TM can be measured experimentally.
Click Here for further information regarding Modifications.
Molar Extinction Coefficient
Optical absorbance at 260 nm is routinely used to measure the concentration of nucleic acids present in a solution. Approximate conversion factors estimate that duplex DNA is about 50 µg/OD260, single-stranded RNA is approximately 40 µg/OD260, and single-stranded DNA is approximately 33 µg/OD260. While this is true for randomized sequence, these conversion factors are less accurate for short oligonucleotides and repeating sequences. Since the absorbance of each base is different, base composition and sequence context influence the absorbance. For example, 1.0 OD260 of d(CCCCCCCCCCCC) (homopolymeric deoxycytidine) has a mass of 39 µg while 1.0 OD260 of d(AAAAAAAAAAAA) (homopolymeric deoxyadenosine) has a mass of 25 µg. The extinction coefficient (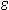 260) describes the relationship between concentration and UV absorbance and can be calculated for any sequence. Greatest accuracy is therefore achieved when the exact value of
260) describes the relationship between concentration and UV absorbance and can be calculated for any sequence. Greatest accuracy is therefore achieved when the exact value of 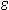 260 is calculated for each oligo. Further, it is possible to take into account the presence of modified groups, such as fluorescent dyes, that have significant absorbance at 260nm.
260 is calculated for each oligo. Further, it is possible to take into account the presence of modified groups, such as fluorescent dyes, that have significant absorbance at 260nm.
The molar extinction coefficient is a physical constant that is unique for each sequence and describes the amount of absorbance at 260nm (A260) of 1 mole/L DNA solution measured in 1 cm path-length cuvette. This definition is derived from the Beer-Lambert law,
A = log(IO / I) =
* c * p
where A is the absorbance, IO and I are, respectively, the intensities of incident and transmitted light, c is the molar concentration of an oligonucleotide (mole/L), p is the length of the light path through the sample (cm), and
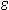 is the molecule molar extinction coefficient (L/(mole
is the molecule molar extinction coefficient (L/(mole
 cm)). The
cm)). The
 260 value of an oligonucleotide is calculated from the following equation
(Cantor,C.R. et al., Biopolymers, 9, 1059-1077., Cavaluzzi,M.J. and Borer,P.N. Nucleic Acids Res., 32, e13),
260 value of an oligonucleotide is calculated from the following equation
(Cantor,C.R. et al., Biopolymers, 9, 1059-1077., Cavaluzzi,M.J. and Borer,P.N. Nucleic Acids Res., 32, e13),
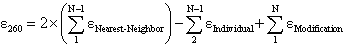
where 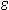 Nearest Neighbor is the nearest neighbor coefficient for a pair of bases,
Nearest Neighbor is the nearest neighbor coefficient for a pair of bases,
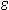 Individual is the coefficient for an individual base, and N is the length of the oligonucleotide.
Individual is the coefficient for an individual base, and N is the length of the oligonucleotide.
See Mixed Base Definitions and Modifications for their effects on 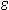 260.
260.
Click Here for further information regarding Molar Extinction Coefficient.
Molecular Weight (Anhydrous)Molecular weight (MW) is the sum of the atomic masses of the constituent atoms for 1 mole of oligonucleotide. The anhydrous molecular weight represents the pure oligo free of any of the counter ions or water molecules that are normally weakly bound to an oligo after synthesis. This calculation gives with the molecular weight measured by mass spectroscopy.
Molecular weight of an oligomer is a sum of the weights of individual bases and chemical modifications. Oligos are typically synthesized without 5’-phosphate group, which must be subtracted.
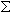 Individual Base MW +
Individual Base MW + 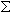 Individual Mod MW - PO2H + H2
Individual Mod MW - PO2H + H2
where PO2H = 63.980 and H2 = 2.016
Molecular weights of DNA bases:
| MWdA | 313.209 |
| MWdC | 289.184 |
| MWdG | 329.208 |
| MWdT | 304.196 |
| MWdU | 290.169 |
| MWdI | 314.194 |
RNA bases: The molecular weight of an RNA nucleotide is the weight of a DNA nucleotide + 15.999, accounting for the additional oxygen atom present (Example: rA is dA (313.209) + 15.999 = 329.208). When determining the weight of uracil (rU) start with dU and not thymine (dT).
2'-O-Methyl bases: The molecular weight of an 2'-O-methyl RNA nucleotide is the weight of a DNA nucleotide + 30.026, accounting for the additional methoxy group (-OCH3) present (For example, mA is dA (313.209) + 30.026 = 343.235). When determining the weight of uracil (mU) start with dU and not thymine (dT).
LNA bases: The molecular weight of an LNA nucleotide is the weight of a DNA nucleotide + 28.011, accounting for the bridging oxygen and carbon from the 2’ carbon to the 4’ carbon (-OCH2-) present (For example, +A is dA (313.209) + 28.011 = 341.220). The exception is LNA C which contains an additional methyl group off of the 5-carbon (14.026).
Phosphorothioated bases: The molecular weight of a phosphorothioate nucleotide is the weight of a nucleotide (DNA, RNA, 2’-O-methyl, LNA) + 16.061, accounting for the substitution of one sulfur atom for a non-bridging oxygen atom in the phosphodiester backbone (For example, A* is A (313.209) + 16.061 = 329.270). Phosphorothioate modification refers to substitutions affecting the internucleoside linkages and does not involve the free 3'- or 5'- ends. Thus a 20-mer phosphorothioate oligonucleotide has 19 phosphorothioate linkages.
See mixed base definitions and modifications for their effects on molecular weight.
nmole/OD260
The amount of oligonucleotide in nanomoles that, when dissolved in 1 mL volume, results in 1 unit of absorbance at 260 nm with a standard 1 cm path-length cuvette. nmole/OD260 is calculated from oligonucleotide's molar extinction coefficient. OD260 is calculated from the following equation,
OD260 = (A260 * V) / p
where A260 is the absorbance at 260 nm, V is the solution volume in mL, and p is the length of the light path through the sample (cm). Thus, OD260 has the units mL/cm. Starting from the oligo molar extinction coefficient,
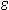 260,
260,
260 = L/(mol
cm) = 103 mL/(mol
cm)
Since OD260 has the units of mL/cm, the equation can be written as,
103 OD260/mol = 103 OD260 / 109 nmol = OD260 / 10-6 nmol
Combination of both equations yields,
260 = OD260 / 10-6 nmol
and this can rearranged as,
Problemnmole/OD260 = 106 /
260
Invalid inputs in the oligonucleotide sequence box are listed in the order from 5' to 3' end of the oligo. The reason for error is displayed. The invalid items are highlighted in red for ease of identification within the sequence.
Secondary SequenceThe formatted input of the oligonucleotide sequence used to hybridize to the primary sequence of interest in the HETERO-DIMER function, shown in 5' to 3' orientation.
SequenceThe formatted input oligonucleotide sequence, which is shown in 5' to 3' orientation.
µg/OD260The amount of oligonucleotide in micrograms that, when dissolved in 1 mL volume, results in 1 unit of absorbance at 260 nm with a standard 1 cm path-length cuvette. µg/OD260 is derived using molecular weight and nmole/OD260 values:
µg/OD260 = nmole/OD260 * molecular weight (g/mol) * 10-3
The definition of OD260 can be found within the nmole/OD260 definition.